利用回朔法求解 0-1 背包问题

我们有 n 种物品，物品 j 的重量为 wj，价格为 pj。我们假定所有物品的重量和价格都是非负的。背包所能承受的最大重量为 c。如果限定每种物品只能选择 0 个或 1 个。有六件物品，体积和价值见下表，背包容量为 25。


i	1 2 3 4 5 6
w(体积)	11 7 9 12 3 10
v(价值)	10 5 7 9 2 12

求解思想：

定义问题解空间；
确定易于搜索的解空间结构，该问题的解空间结构为子集树；

回朔法

采用深度优先方式搜索解空间，同时要及时剪枝，避免无效搜索。该问
题的限界函数为：

public class _01KnapsackProblem {
    public int[] weight;
    public int[] value;
    public int[] take;

    int curWeight = 0;
    int curValue = 0;

    int bestValue = 0;
    int[] bestChoice;
    int count;

    int maxWeight = 0;

    public void init(int[] weight, int[] value, int maxWeight) {
        if (weight == null || weight.length == 0
                || value == null || value.length == 0
                || weight.length != value.length || maxWeight <= 0) {
            System.out.println("输入数据有错！");
            return;
        }
        this.value = value;
        this.weight = weight;
        this.maxWeight = maxWeight;
        count = value.length;
        take = new int[count];
        bestChoice = new int[count];
    }

    public int[] maxValue(int x) {
        //走到了叶子节点
        if (x > count - 1) {
            //更新最优解
            if (curValue > bestValue) {
                bestValue = curValue;
                for (int i = 0; i < take.length; i++) {
                    bestChoice[i] = take[i];
                }
            }
        } else {
            //遍历当前节点（物品）的子节点：0 不放入背包 1：放入背包
            for (int i = 0; i < 2; i++) {
                take[x] = i;
                if (i == 0) {
                    //不放入背包，接着往下走
                    maxValue(x + 1);
                } else {
                    //约束条件，如果小于背包容量
                    if (curWeight + weight[x] <= maxWeight) {
                        //更新当前重量和价值
                        curWeight += weight[x];
                        curValue += value[x];
                        //继续向下深入
                        maxValue(x + 1);
                        //回溯法重要步骤，个人感觉也是精华所在。
                        // 当从上一行代码maxValue出来后，需要回溯容量和值
                        curWeight -= weight[x];
                        curValue -= value[x];
                    }
                }
            }
        }
        return bestChoice;
    }
    public static void main(String[] args) {
        _01KnapsackProblem bt=new _01KnapsackProblem();
        bt.init(new int[]{11,7,9,12,3,10},new int[]{10,5,7,9,2,12},25);
        int[] result = bt.maxValue(0);
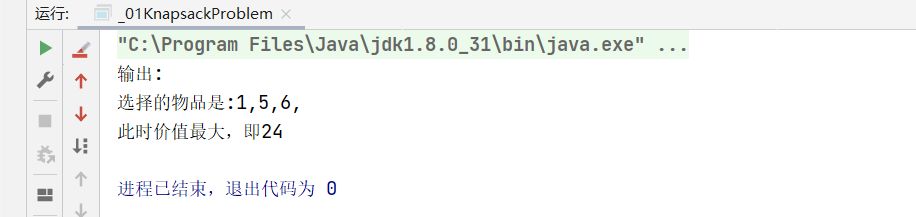
        System.out.print("输出:\n"+"选择的物品是:");
        for (int i = 0; i <=bt.bestChoice.length-1 ; i++) {
            if (bt.bestChoice[i] == 1) {
                System.out.print(i+1+",");
            }
        }
        System.out.println("\n此时价值最大，即"+bt.bestValue);
    }
}