多段图问题
若存在一个有向加权图 G,且 G 能分出起点和终点以及中间的 n 的阶段,求起点到终点的最短(长)距离。
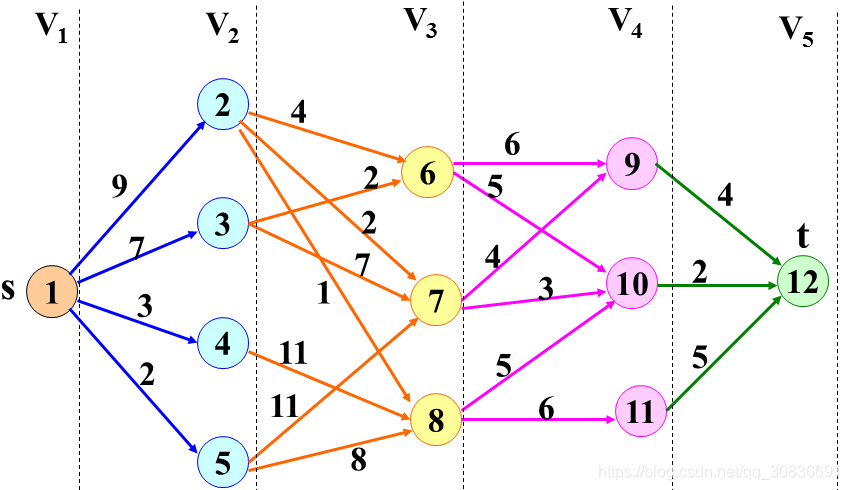
求解的思想:
- 将图中的顶点划分 5 个阶段,k
- 每个阶段有几种供选择的点 s
- 当前状态应在前一个状态的基础上获得。决策需要满足规划方程
规划方程:f(k)表示状态 k 到终点状态的最短距离。
初始条件:f(k)=0,k=0;
f(k-1)=min{f(k)+W(k-1,k)}其中 W(k-1,k)表示状态 k-1 到状态 k 的距离※※※※以下代码用的向前处理法与老师不同,但都是最短路径※※※※ 运行结果:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69public class Duoduantu {
static int N = 13, K = 5, INF = 1000;
static int[][] c = new int[N][N]; //c[i][j]表示i到j的花费
static int[] cost = new int[N]; //cost[i]表示到结点i的最小花费
static int[] d = new int[N]; //d[i]表示由结点i指向的最小成本边的另一端的结点
static int[] P = new int[K]; // 每一阶段最短路径成本
public static void main(String[] args) {
List<Integer> list = new ArrayList<Integer>();
init(); //初始化
fGraph();
int k = K;
int sum = 0;
int n = N - 1;
while (k != 1)//遍历每个阶段的最短路径成本
{
sum += cost[n];
n = d[n];
list.add(n);
k--;
}
System.out.println("输出:" + "\n" + "最短路径为:");
for (int i = list.size() - 1; i >= 0; i--) {
System.out.print(list.get(i) + "->");
}
System.out.println("12");
System.out.println("最小成本路径为:" + sum);
}
public static void fGraph() {
int min;
for (int j = N - 1; j > 0; j--)//向前处理方法
{
min = INF;
//for (int i = 1; i < N; i++)
for (int i = j - 1; i > 0; i--)//从j - 1开始可以减少比较次数
{
if (c[i][j] != INF && cost[j] + c[i][j] < min)//找出结点r, 满足<j, r>∈E且使c(j,r)+COST(r)值最小
{
min = cost[i] + c[i][j];
d[j] = i;
}
}
cost[j] = min;//数组cost[i]保留到结点i的最短边的权值
}
}
public static void init() {
for (int i = 1; i < N; i++) {
cost[i] = 0;
for (int j = 1; j < N; j++) {
c[i][j] = INF;
}
}
//为了测试方便,直接码出来了
c[1][2] = 9;c[1][3] = 7;c[1][4] = 3;c[1][5] = 2;
c[2][6] = 4;c[2][7] = 2;c[2][8] = 1;
c[3][6] = 2;c[3][7] = 7;
c[4][8] = 11;
c[5][7] = 11;c[5][8] = 8;
c[6][9] = 6;c[6][10] = 5;
c[7][9] = 4;c[7][10] = 3;
c[8][10] = 5;c[8][11] = 6;
c[9][12] = 4;
c[10][12] = 2;
c[11][12] = 5;
}


