最小生成树

Prim 算法计算最小生成树。最小生成树的定义：最小生成树是一副连通加权无向图中一棵权值最小的生成树。假设给定无向图 G 一共有 n 个顶点，那么最小生成树一定会有 n-1 条边。

无向图

求解思想：

选定一个点做为一个集合 a，剩下的点为另一个集合 b；
将横跨两个集合且权重在其中最小的边加入最小生成树；
将刚刚加入最小生成树的边中不在集合 a 中的点加入集合 a，直到所有的点加入集合 a。

MGraph类

public class MGraph {
    /*图的邻接矩阵表示*/
    int nodes;  //图中结点数目
    char data[];  //存放结点数据
    int[][] weight;  //存放边

    public MGraph(int ve) {
        nodes = ve;
        data = new char[ve];
        weight = new int[ve][ve];
    }
}

MinTree类

public class MinTree {
    private static int sum = 0;//最小权值

    /*创建图的邻接矩阵*/
    public void CreateGraph(MGraph graph, int nodes, char data[], int[][] weight) {
        int i, j;
        for (i = 0; i < nodes; i++) {
            graph.data[i] = data[i];
            for (j = 0; j < nodes; j++) {
                graph.weight[i][j] = weight[i][j];
            }
        }
    }

    public void Prim(MGraph graph, int v) {
        /*graph为图的邻接矩阵表示，v为起始顶点*/
        int[] visited = new int[graph.nodes];  // visited[]标记结点是否被访问过
        for (int i = 0; i < graph.nodes; i++) {   //初始化visited[]
            visited[i] = 0;
        }

        visited[v] = 1;
        int h1 = -1, h2 = -1;   //记录边的弧尾和弧头
        int wineWeight = 10000;//minWeight记录最小权重
        for (int k = 1; k < graph.nodes; k++) {  //nodes个顶点，最小生成树中有nodes-1条边

            for (int i = 0; i < graph.nodes; i++) {  //i顶点表示被访问过的顶点
                for (int j = 0; j < graph.nodes; j++) {  // j顶点表示未被访问过的顶点
                    if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < wineWeight) {
                        //寻找已访问的顶点与未访问的定点间的权值最小的边
                        wineWeight = graph.weight[i][j];
                        h1 = i;
                        h2 = j;
                    }
                }
            }

            System.out.println(graph.data[h1] + "," + graph.data[h2]);
            sum += wineWeight;
            visited[h2] = 1;   //标记h2被访问过
            wineWeight = 10000;
        }

    }

    public static void main(String args[]) {
        char[] data = new char[]{'1', '2', '3', '4', '5', '6'};
        int nodes = data.length;
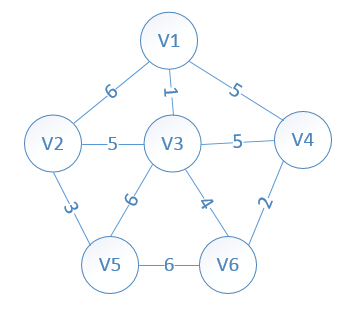
        int[][] weight = new int[][]{
                {0, 6, 1, 5, 10000, 10000},
                {6, 0, 5, 10000, 3, 10000},
                {1, 5, 0, 5, 6, 4},
                {5, 10000, 5, 0, 10000, 2},
                {10000, 3, 6, 10000, 0, 6},
                {10000, 10000, 4, 2, 6, 0}
        };
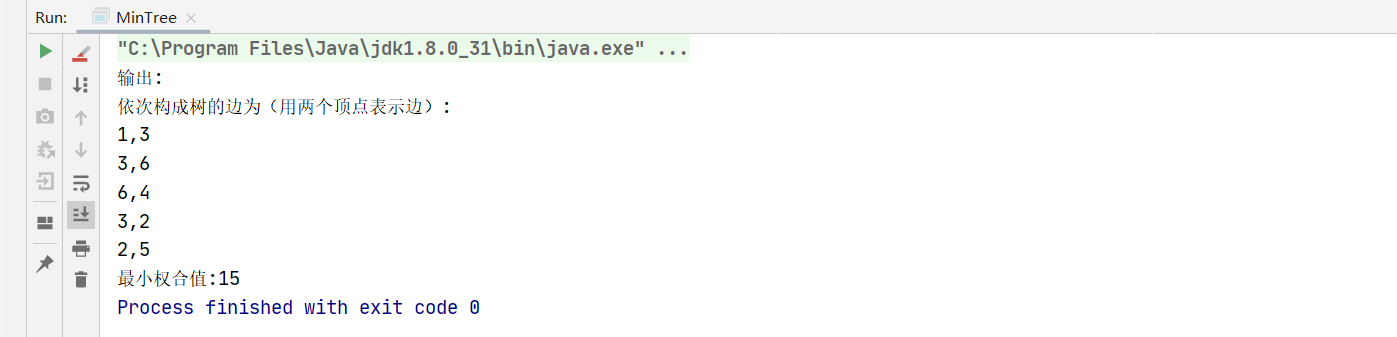
        System.out.println("输出:\n" + "依次构成树的边为（用两个顶点表示边）:");
        MGraph graph = new MGraph(nodes);//初始化邻接矩阵
        MinTree mt = new MinTree();//初始化最小生成树
        mt.CreateGraph(graph, nodes, data, weight);//创建邻接矩阵，graph:临界矩阵类型, nodes:节点数, data:结点名字, weight:权值
        mt.Prim(graph, 0);//
        System.out.print("最小权合值:" + sum);

    }
}